본문으로 건너뛰기

1 Floyd Warshall Algorithm​

  • 플로이드-워셜 알고리즘은 가중 그래프에서 모든 노드 쌍 사이의 최단 경로를 계산하는 데 사용됩니다.
  • 이는 방향 그래프와 무방향 그래프 모두에 적용됩니다.

알고리즘의 주요 특징

  • 모든 노드 쌍 사이의 최단 경로를 계산합니다.
  • 그래프를 표현하기 위해 인접 행렬 방식을 사용합니다.
  • 다이나믹 프로그래밍 기법에 속합니다.

2 점화식​

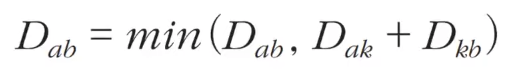
image-20220623135454497

  • 플로이드-워셜 알고리즘의 핵심은 모든 노드 쌍에 대해, 가능한 모든 중간 노드를 거쳐 가며 최단 경로를 업데이트하는 것입니다.
  • 이 과정에서 사용되는 점화식은 위와과 같습니다
  • a에서 b로 가는 최단 거리보다 a에서 k를 거쳐 b로 가는 거리가 더 짧은지 검사합니다.

3 동작방식​

  1. 먼저 2차원 테이블 D를 초기화합니다.
    1. D[a][b] = a에서 b까지의 거리
    2. a에서 b로 가는 경로가 없는 경우 INF 값으로 초기화합니다.
  2. 인접 정점 간의 최소 거리로 테이블 갱신

3.1 단계별 동작 방식​

초기 상태 (k=0)

  • 아직 어떤 정점도 거치지 않은 상태입니다.
  • 오직 직접 연결된 간선의 가중치만 고려됩니다.
  • 직접 연결되지 않은 정점 쌍은 무한대(INF) 값을 가집니다.

첫 번째 정점을 거치는 경우 (k=1)

  • 1번 정점을 중간 경유지로 고려합니다.
  • 모든 정점 쌍 (a,b)에 대해 다음을 비교합니다:
    • 현재 a에서 b로 가는 거리
    • a에서 1번 정점을 거쳐 b로 가는 거리
  • 더 짧은 경로가 있다면 거리를 갱신합니다.

두 번째 정점을 거치는 경우 (k=2)

  • 2번 정점을 중간 경유지로 고려합니다.
  • 이전 단계에서 1번 정점을 거쳐 가는 경로가 갱신된 상태에서:
    • 현재 a에서 b로 가는 거리
    • a에서 2번 정점을 거쳐 b로 가는 거리
  • 를 비교하여 더 짧은 경로로 갱신합니다.

3.2 예제 코드​

import sys

input = sys.stdin.readline

V = int(input())
E = int(input())

## #정점 간의 최소 거리는 나타내는 2차원 배열 초기화
distance = [[sys.maxsize] * (V + 1) for _ in range(V + 1)]
for i in range(V + 1):
    distance[i][i] = 0

## #인접한 정점의 최소 거리로 2차원 배열 갱신
for _ in range(E):
    vertex1, vertex2, weight = map(int, input().split())
    distance[vertex1][vertex2] = min(distance[vertex1][vertex2], weight)

## #i: 거쳐 가는 정점
for i in range(1, V + 1):
    # j: 출발 정점
    for j in range(1, V + 1):
        # k: 도착 정점
        for k in range(1, V + 1):
            # j에서 k를 가는 비용 보다 j 에서 i를 거쳐 k로 가는 비용이 더 적다면 갱신
            if distance[j][i] + distance[i][k] < distance[j][k]:
                distance[j][k] = distance[j][i] + distance[i][k]

4 시간복잡도​

  • O(V³)의 시간복잡도를 가집니다.
    • V는 정점의 개수입니다.
    • 3중 반복문을 사용하기 때문입니다.
  • 노드의 개수가 적은 경우에 효율적입니다.
  • 노드가 많은 경우에는 다익스트라 알고리즘을 고려하는 것이 좋습니다.

5 전이 폐쇄(Transitive Closure)​

  • 플로이드-워셜 알고리즘은 최단 경로 찾기 외에도 그래프의 전이 폐쇄(Transitive Closure)를 찾는 데 활용될 수 있습니다.
  • 전이 폐쇄란 "A→B이고 B→C이면 A→C이다"와 같은 추론이 가능한 관계를 의미합니다.

5.1 대표적인 예시 문제 설명​

  • 프로그래머스 순위 참고
  • n명의 권투 선수가 대회에 참여합니다.
  • 각 선수는 1번부터 n번까지 번호를 부여받습니다.
  • 실력이 더 좋은 선수는 항상 실력이 낮은 선수를 이깁니다.
  • 일부 경기 결과만 주어질 때, 정확한 순위를 매길 수 있는 선수의 수를 찾습니다.

5.2 해결 방법​

def solution(n, results):
    # 승패 관계를 저장할 2차원 배열 초기화
    graph = [[0] * (n + 1) for _ in range(n + 1)]
    
    # 승패 관계 입력 (1: 승리, -1: 패배)
    for winner, loser in results:
        graph[winner][loser] = 1
        graph[loser][winner] = -1
    
    # 플로이드-워셜로 추가적인 승패 관계 파악
    for k in range(1, n + 1):
        for i in range(1, n + 1):
            for j in range(1, n + 1):
                if graph[i][k] == 1 and graph[k][j] == 1:
                    graph[i][j] = 1
                    graph[j][i] = -1
    
    # 순위를 정확히 알 수 있는 선수 수 계산
    answer = 0
    for i in range(1, n + 1):
        if sum(1 for j in range(1, n + 1) if graph[i][j] != 0) == n - 1:
            answer += 1
    
    return answer

5.3 적용 원리​

  • 직접적인 승패 관계를 1(승리)과 -1(패배)로 표시합니다.
  • 플로이드-워셜 알고리즘으로 간접적인 승패 관계도 파악합니다.
  • "A가 B를 이기고, B가 C를 이기면, A는 C를 이긴다"는 추론이 가능합니다.
  • 모든 다른 선수들과의 승패를 알 수 있는 선수만 순위가 확정됩니다.

참고 자료